|
Ontology Based Document Understanding
Notate 96 Conference
Paul S. Prueitt, PhD
Senior Scientist
Knowledge Processing Project
Highland Technologies Inc.
paul@htech.com
This paper is modified from a chapter in "Knowledge
Processing, A new toolset for Data Mining", an internal Highland
Technologies document. The paper starts out by delineating the
basis for ontology based document understanding. The first two
sections address hard questions in knowledge representation.
We have tried to present this material in such a way as to enable
the first time reader to move ahead to the later sections. These
sections can be skipped on first reading, but their content is
required to understand the full import of the material that follows.
The third section maps out the extraction of theme vectors from
Oracle's ConText NLP product and links natural language processing
to the formation of a class of natural kind. The fourth section
is on the use of formal models as defined by Dmitri Pospelov.
The fifth section walks the path required to produce a formal
model from the linguistic analysis of text. The next two sections
briefly treat the issues of (1) multiple ontology and (2) knowledge
processing units as a classification engine. The last section
introduces the procedure for constructing a periodic table of
subfeatures for a given class of situations.
What is an ontology?
A machine readable ontology is a sophisticated version
of a semantic net, in which concepts are identified with nodes
and relationships between concepts are identified as linkage.
Semantic nets are sufficient to understand a class of well formed
text where semantics is about very static situations. Comparative
terminology science, under development by Faina Citkina, identifies
two sets of conditions under which text understanding can not
be achieved by static ontology. The first condition is where
a shift in meaning, from the static case, is required to account
for circumstances of a specific situation. The second condition
is when interpretative rules given by a selected static ontology,
even when slightly modified, will always produce an error in interpretation.
The architectural design for text understanding must take both
of these possible conditions into account, and does so with a
theory about the natural compartmentalization of processes in
the world.
The issue of translatability, between one natural
language into another natural language, identifies the types of
issues that machine understanding systems are facing. Some of
these issues may be addressed if we have machine readable ontology.
A single formal representation of ontology is not, however, sufficient.
We can describe conditions for semantic alignment under circumstances
where the target and source text are both "interpreted"
by correspondences to the combination of two, perhaps distinct,
ontologies. What is required is the integration of two or more
compartmentalized sets of rules and objects into a new compartment.
This is like the joining of two opposing points of view into
one that subsumes both. Integration is more likely to occur if
it takes place within a larger context and the opposing views
are entangled in this context. Tracing the entanglement of two
ontologies within a specific situation is a difficult matter.
The joining of distinct ontologies will trigger a finite number
of paradoxes that must be resolved by known facts about the situation.
A system that resolves these paradoxes will produce information
complimentarity and the emergence of a new system for understanding
both ontologies and their natural inter-relationships. A theory
of differential ontology helps handle these critical problems.
Differential ontology aids text summarization and
generation systems as well as text translation and situational
modeling. The theory of process compartments, each compartment
having its own ontology, provides a means to ground differential
ontology to compartmentalized network dynamics. A mathematical
framework based on weakly coupled oscillators illustrates the
variety of structural outcomes from differential geometry. If
ontology is associated with a compartment, and multiple compartments
are possible, then the theory of process compartments provides
a means to understand why some concepts are easily translated
while others might not be translatable without significant effort.
However, the assumption that multiple compartments exist is not
justified easily.
The nature of paradox, complimentarity and emergence
have physical correlates that are studied at the quantum level
by physicists. It is not too much to expect help from this community.
Quantum physics is a mature science that has faced a number of
hard problems of this type. We can borrow some of the formal
tools, developed to study elementary particle interaction, and
extend quantum mechanical analytical methods to address the hard
problems found in computational document understanding. First,
we borrow the notion that a finite and quantal distribution of
possible interpretations is driven by an underlying, and knowable,
organization of the world. This enables the disambiguation of
meaning, in most cases. In cases where novel emergence must occur
in order to find an appropriate container for representation;
then we hope to use the notion of entanglement and the formation
of a new compartments through complimentarity and observation.
Dmitri Pospelov identified, in the early 1960s,
a flaw in modern control theory based on formal systems. Independent
Western researchers, like Robert Rosen, have also identified this
flaw. Formal systems require a closure on what can be produced
from rules of inference about signs and relationships between
signs. This means that the formal system, no matter how well
constructed, will not always be able to perfectly model the changes
in a non-stationary world. Biological systems, however, are capable
of constructing new observables through a process of perceptional
measurement. How is this accomplished?
Peter Kugler defines perceptual measurement as the
construction of world views by biological systems. His recent
work addresses the issues of observation, complimentarity, emergence
and entanglement. He concludes that the origins of semantic functions,
relationships between symbols and the external world, is perceptional
measurement. Kugler's experimental results has shown examples
where a change in a point of reference will cause a shift in perceptual
measurement and thus in the semantics of things observed. He
hypothesized that the point of reference uses epistemology to
localize facts about the world into a synthesized ontology specific
to a situation. Kugler's work with Russian neuroscientist, Juri
Kropotov, tracks this localization to structural properties seen
in human cortical architecture and recently implemented into pattern
recognition software.
Classification of issues regarding computational
document understanding:
Faina Citkina has created a classification for treating
issues of translatability. In her classification schema, there
are three types of terminological relativity; referential, pragmatic
and interlingual. The Citkina classification will be used to
discuss issues that arise in computational document understanding.
Special texts, like product manuals, often have
one to one correspondences to devices or processes. The issue
of their understanding, and thus their translatability, is included
in a class of interlingual type terminological relativity, since
there is a clear external object for each concept expressed.
Technical jargon would appear to have the same distinction, at
least on the surface. A poem might have less clear reference
to external objects and minimalist art would have even less correspondence
to a finite and specific set of things in the world.
The Citkin class of interlingual issues can
only be resolved if a knowledge domain has been encoded to allow
automated checking procedures between the source text and the
target text. The knowledge domain can be something like an expert
system or object database, but these knowledge sources are not
open systems and thus will fail unpredictably. Since telling us
about the failure may also not occur, the system will, as it were,
lie to us on a fairly regular basis. The knowledge domain can
be a semantic net or an ontology like a semiotic table, in which
case the possibility for document understanding and thus translation
of meaning is enhanced.
The Citkin class of pragmatic issues is also
related to a theory of interlingua where the situation addressed
is dynamic. The Highland approach assumes the necessary existence
of a period table where the system states that a compartment can
assume are all specified and related to a database of subfeatures.
The properties of this periodic table is representable in the
form of a second database plus situational language and logic.
Developing the table, the situational language and the logic
is an almost inconceivable task, were it not for the work of semioticains
D. Pospelov and V. Finn. However, in the case of Finn's system
for structural pharmacology and several other proprietary systems,
this work has been done and can be demonstrated. The Pospelov-Finn
systems have the ability to produce an "emergent" ontology
for situations where pragmatic and interlingua issues characterize
the hard tasks. In this case, when the tools are available, the
emergent ontology is computable.
An underlying ontology, as expressed in a semantic
net or table, can assume different system states and thus the
sense of the terms may drift. This would imply that the rules
that govern an ontology would allow a modification of the sense
of the target term so that the text would be understood in a sense
that is consistent with the source term. Here the translation
process must import some of the knowledge that tracks this drift
in sense, but the target representation would be (almost) semantically
invariant to the source representation.
Thus pragmatics is, as it should be, related only
to a specific situation at a specific time (or state of the ontology).
Interlingua type relativism is a condition of equality, i.e.,
this word is that word. Pragmatic type relativism is a condition
of system transitions from one state into another, but under a
uniform set of rules. As demonstrated by Pospelov and Finn, this
set of rules can be captured in the special semiotic logics of
applied semiotics.
The Citkin class of referential type include
issues arising where a term's meaning in the source language has
an ontology that does not exist in the target language. Here
the process compartment that shapes the source term's meaning,
in the world of someone's experience, does not correspond to a
neural processing compartment, responsible for generating signs
in the target language.
An example would be the ontology created by scientific
deference to Marx and Pavlov's scientific materialism in post
World War II USSR. In the West there was no such deference, or
at least the deferences were of a different type. Western evaluation
of much of the ontology of Russian Information Operations (RIO)
technology have no corresponding English signs. We can predict;
therefore, that RIO will continue to be a mystery to American
IO, and vice versa. A second example is the deference given to
two valued logic by Western philosophers and scientists. This
deference is deeply grounded in our culture. In the West, the
notion that non Boolean logic would be of "ontological"
value is ridiculed. A third example would be the structure and
form of Hopi sand (medicine) drawings. Most people unaware of
Indian "Old Way" would never imagine that a relationship
could be made between colored sand designs and the healing process.
In each of these examples, the problem with translatability is
that there are no containers to place meaning in target languages,
unless that language has a similar referential type.
Mining for raw resources
The first two sections communicates the general
principles that shape the theory and practice of knowledge processing.
In the next section, we develop the notation and architecture
for extracting concepts from the thematic analysis of document
collections.
Let C be a collection of documents, T
the set of ConText computed theme vectors, and I the inverted
index for T, (see figure 1.)
T contains a set of theme
vectors,
T = { (n, wp)j
| dj e C
}
where di is a document, n = { n1
, . . . , n16 } and wp = { wp1 , . . .
, wp16 }. The positive integer ni is the
semantic weight of the theme wpi .
Figure 1: Each document
in a collection C is represented by a vector of weights
and phrases. The full set of theme vectors T is represented
as an inverted index I of merged Oracle ConText Option
(OCO) classifications.
ConText Knowledge Catalog supports an automated
procedure that uses an index of OCO classifications to produce
a means to classify a collection of documents based on computed
themes and user defined views of a knowledge domain. User views
are expressed as traditional hierarchical taxonomies or as a semantic
net.
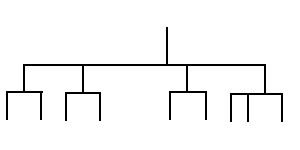
(a)
| 
(b) |
Figure 2: User
views can take the form of a simple hierarchy (a) or as a more
complex semantic net (b)
To add value to OCO classifications, we first refine
the representation architecture to produce a set of distinct situational
specific ontologies, and then derive a theory of differential
ontology to manage these as data sources. We are interested here
in a computational architecture for knowledge extraction and representation.
A neural network architecture for simulating selective attention,
attraction to novelty and the production of choice is presented
in publications with mathematician Dan Levine (see, for example,
Levine, Parks & Prueitt, 1993, Methodological and Theoretical
Issues in Neural Network Models of Frontal Cognitive Function,
in International Journal of Neuroscience, 72 209-233.)
A basis in the research of neuroscientist Karl Pribram for an
multilevel, biologically feasible, architecture for compartmental
processing of information has been developed but not yet implemented.
The method presented below is a modification of
several published methods for identifying concepts using vector
representation of documents. It borrows features from Hecht Nielson's
method based on word stemming plus vector clustering, Oracle ConText
Option (OCO) method for construction Knowledge Catalogs, and D.
Pospelov - V. Finn methods for situational representation.
A schematic diagram,
showing the architecture for knowledge extraction, is drawn in
Figure 3. C, and T have been introduced above.
S is the representational space for the collection's
theme vectors. S is formally a simple Euclidean space with,
for moderate size collections in one subject field, about 1500
dimensions. Each dimension is created to delineate a single theme
phrase. Subject fields with greater than 1500 themes should be
compartmentalized into a small number of topic areas. The relationships
between topic areas and the topics need to be separated into manageable
groups.
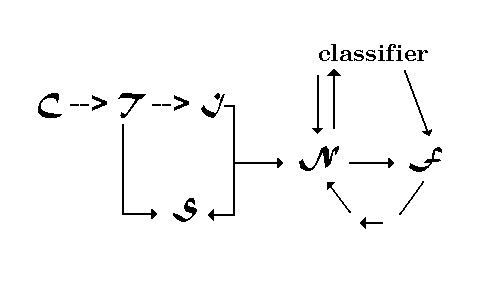
Figure 3: Schematic
diagram for knowledge extraction and situational representation
Suppose that we have a document collection C
about a small number of narrow topics. Let T be the set
of ConText generated theme vectors. The phrase component of each
vector component for every element in T can be sorted into
bins. New bins are created when necessary so that each bin is
representative of a single theme and every theme has been placed
in a bin. This process creates an "inverted index"
of the themes. The inverted index is ranked by the number of
documents having that theme. This ranked index is denoted by
the symbol I.
I = { ti
| i e index
set J }
Now a user can fix a view of the document collection
by marking as "valid" all themes having relevance to
that view. This procedure is, of course, based in an intuitive
judgment by a user. Software can make the judgment easy to execute,
and can allow multiple views to be specified. As we will see,
changes in defined views are computationally easy since these
changes do not depend on a recomputation of theme vectors.
The valid themes for a view define a subspace Sview
. This subspace can be used for trending of synthetic concepts
as defined in Chapters 1 and 2 of "Knowledge Processing,
A new toolset for Data Mining". The inverted index I
can be restricted to the valid themes for a specific view.
The result is a new inverted index denoted here by the symbol
J.
J = { ti
| i e index
set K which is a subset of the set J}
An assertion can be made about the completeness
of Sview as a representational space with respect
to a knowledge domain. If the collection of documents is comprehensive
then additional computation of theme vectors for new documents
will not increase the dimension of Sview .
This is because the process of creating new bins for themes will
saturate if the size of N is finite.
N denotes a class of
natural kind. It is an inventory of all of the things that are
constituents of events that rise in a specific arena. For example,
a list of all man made pharmacological agents would be a class
of natural kind. The set of all atomic elements is another class
of natural kind. And under certain circumstances, the set of
validated themes J is also a class of natural kind. A
theory of how the elements of a class are created requires a list
of subfeatures and a theory about how the parts of an elements
are aggregated to form a whole. We will return to this point
later when we discuss the so called "derived model"
in the last section.
N can be thought of as
the situations that arise from J. These situations are
often associated with concepts in the form:
concept = { ti
| i = 1, . . , k }
where ti is associated with an element
in the set of subfeatures J. This is our model for document
understanding.
The use of formal models and semiotic models:
In Chapter 1, "Trending Analysis with Concept
Trends" of "Knowledge Processing", we introduced
general notion for a synthetic concept with n components:
concept = { ai
| i = 1, n }
where ai is a theme phrase. With this
very simple construction it is possible to view the occurrence
of the full concept or even individual themes within a single
synthetic concept. The problem is, of course, that the concept
has not been validated as meaningful. In what follows, we will
integrate the notion of a formal system with some techniques for
refining the description of a meaningful concept.
A history of formal and semiotic systems is given
in D. Pospelov's book, Situational Control: Theory and Practice,
published in Russian by Nauka in 1986. We have worked from a
translation produced in 1991, and from a number of articles by
Pospelov and Victor Finn and their students. We have also been
able to discuss some issues in person with Pospelov and Finn.
Our effort has been to synthesize Russian applied semiotics with
Western artificial intelligence and the theory of natural language
processing. Our purpose is to build a natural language pre-processor
for computational knowledge processing based on ontology. The
semiotic systems demonstrated to us by the Pospelov - Finn group
has shown us that ontologies can be created using the extensive
logical theory and heuristic methods developed by the Russian
community. In what follows, we will make reference by name to
individuals who either communicated a technique to us or published
material describing this technique. However, a presentation of
the research literature will be left for future work.
The notion of a synthetic concept arises rather
naturally once the very hard task of generating theme vectors
is completed. For us this is done using the Oracle ConText Option
(OCO). ConText computes a set of linguistically weighted theme
vectors T. Once this is done, the question of where the
theme vectors came from is not important. However, this step
is accomplished with an advanced natural language processor (NLP)
having a rich knowledge of the world and language. If used in
a certain way, the NLP can replace a time intensive step that
Pospelov was required to make to produce his formal models. In
Situational Control (pg 32) Pospelov states; "situational
control demands great expenditures for the creation of a preliminary
base of data about the object of control, its functioning and
methods of controlling it." This step can be automated using
ConText type technology.
Consider the case where our document collection
contains diplomatic messages regarding the internal affairs of
a country, industry, company, computer network, social situation,
medical case, etc. This collection of messages is collected into
a document database which is then indexed using ConText. A set
T of theme vectors is produced. From this set of theme
vectors we can easily merge the individual theme phrases into
a table and count the number of messages having a specific theme.
This produces an occurrence ranked inverted index I on
the message themes. An expert on the internal affairs of the
country is asked to mark those themes that are of most interest
from a certain point of view. This produces a new inverted
index containing themes of interest. These themes can be quickly
converted into either a hierarchical taxonomy, perhaps with "see
also" hyperlinks, or a semantic net. One purpose for constructing
ConText knowledge catalogs is to provide a means to classify documents
by user validated themes. The nodes of the semantic net, or taxonomy,
are linked to names of files by HighView, our document management
software. The resulting system has a means for displaying the
collection of documents by thematic content and for retrieving
documents from that display.
We have developed an additional capability. To
understand this capability, we return to the definition of Pospelov's
formal systems (Situational Control , pg 36):
Definition: The term formal
system refers to a four-term expression:
M = < T, P, A, R>
where T = set of basic elements, P = syntactic rules,
A = set of axioms, and R = semantic rules. The interested reader
can refer to Situational Control for a more detailed treatment
of formal systems. For our purposes we need only refer to a figure.
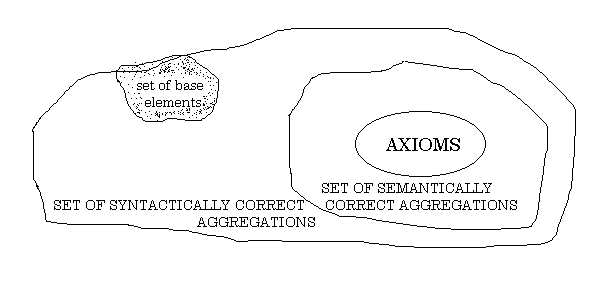
Figure 4: Taken
from Figure 1.8, Situational Control (pg 37)
In figure 4, the set of base elements T are combined
in various ways to produce three type of sets, axioms, semantically
correct aggregates, and syntactically correct aggregates. We
should remember that mathematical logic is founded on a similar
construction and therefore that most of the results of mathematical
logic will somehow apply later on to the theory of knowledge processing
that we are constructing. For example, the set of axioms can
be specified to consist of independent, non contradictory and
self evident statements about the set of base elements T. Rules
of inference can also be formulated to maintain notions about
true or false inference from assignments of a measure of true
to the axioms. The set of syntactically correct aggregations
of elements of base elements can be defined either by listing
or by some implicit set of rules. The semantically correct aggregations
could then be interpreted as those syntactically correct aggregations
that have an assignment of true as a consequence of the inference
rules. However, this interpretation is only one of a number of
interpretations for the formal relationships between T, P, A,
and R.
We have found a simplification of theory and reflected
this in our software. Pospelov himself notes that the axiom set
can be the same as the set of semantically correct aggregations.
In this case the rules of inference need not be known, but we
certainly will lose the property that the axioms be independent
and the axiom set be minimal in size. In the case where the system
under study is a natural complex system, such as a national economy,
there is no fully understood set of inference rules. One can
only observe that the economy experiences modal changes from one
condition into another. Each condition can be defined "phenomenologically"
as a semantically correct aggregation of an unknown or partially
unknown set of base elements. We view only the surface features.
Given this caveat, we will define the following formal model.
Definition of a formal model from theme phrases:
Let T = J . T is now the set of theme phrases
that have been chosen by an expert as representative of the expert's
view of the situations addressed by the messages. The size of
T, denoted by |T|, is finite and small - perhaps less than 300
elements. Let P be the set containing a single syntactic rule
stating that any subset of T will be considered a syntactically
correct aggregation. Of course the size of the set of syntactically
correct aggregations is 2^300, which is a very large number. At
this point we have a lower and an upper envelop on the semantic
rules. Any possible semantic rule must assign the possibility
of being meaningful to an element of the "power set"
.
It is noted that one way to specify a set of semantic
rules is to explicitly list the semantically correct aggregations.
Let A, the set of axioms, be defined to be equal to the set of
semantically correct aggregations.
T, P and A so defined leave only one remaining definition.
The definition for the set of axioms is a boot strap, since at
this point there is no means for identifying which of the syntactically
correct aggregations of base elements are meaningful, with respect
to the view under consideration. We need to create the semantic
rules.
In Chapter 2 of "Knowledge Processing",
we introduced the notion of stochastic clustering of theme vector
representations of documents. We define a semantic rule that
states the following: If a subset of T is grouped together by
a clustering procedure, then the subset is meaningful. Such a
rule would reduce the number of "candidate" semantically
correct aggregations from 2^300 to a much smaller number, perhaps
2,000. However, such a rule is dependent on pairwise measures
of similarity based theme vector distance. Selecting good pairwise
measures of distance is an interesting problem that has been worked
on by a number of researchers. This problem is equivalent to
the construction of a good axiom set and proper rules of inference.
We are interested in bypassing this problem by employing any
reasonable pairwise measure and then employing "checking"
procedures to validate potentially meaningful aggregations. What
results is a compound semantic rule with two parts, (1) clustering
and (2) checking.
To summarize our compound semantic rule: a set
of themes serves as subfeatures to be aggregated using an algorithm
to cluster theme vectors, as in Chapter 2 of "Knowledge Processing".
When vector clustering identifies a collection of theme vectors
as being close, then the individual themes within those theme
vectors are grouped together as a syntactically correct aggregation.
The aggregation is treated as a synthetic concept and checked
to see if the synthetic concept is meaningful. Checking for meaning
can be as simple as asking the expert if the synthetic concept
is suggestive of the situations known to exist and referenced
by the message collection.
At least one automated checking procedure has been
identified. Synthetic concepts can be trended over feature sets,
such as a time sequence, to see if temporal distributions reveal
locally normal profiles, see figure 18 page 12 of "Knowledge
Processing". Other visualization methods are clearly possible
and have the advantage that a user is able to use human intuition
to organize and structure the set A of axioms.
In Pospelov's book, Situational Control,
he describes methods for "deconstructing the set A and reconstructing
an new minimal size axiom set A' and rules of inference that will
generate from A' a copy of A. In this case the formal model has
an good axiom set and the inference rules are able to generate
conjectures about new aggregations not originally in A, but from
the same situation. This enables computational knowledge generation
as demonstrated by the Russian semiotic systems.
Working with multiple classes of natural kind:
Each of the seven objects in Figure 3 have an independent
role and can be stored separately. For example, J , Sview
, and N can be stored in a small computer space and called
into being when the original view of a document collection is
appropriate. This enables a process compartment approach towards
text understanding. The compartment in this case is called a
Knowledge Processing Unit (KPU), Figure 6.
It is important to note that a compartmentalization
of document views into classes of natural kind is operationally
independent of ConText lexicon and knowledge catalog resources.
An iterative feedback between a KPU and ConText would focus the
linguistic analysis and produce better results.

Figure 6: Iterative
feedback between a Knowledge Processing Unit (KPU) and ConText
This focus will improve the performance of a particular
KPU.
The use of KPU as classification engine:
A single KPU can be used as a classification engine.
The computation involved is minimal, except for ConText computation
of a theme vector. The theme vector can be placed into a visual
representation of the classes of natural kind, for example using
the Spires software package. If Spires is not available, the
vector distance between the center of the concept for each natural
kind and the new theme vector is computed and classification made
accordingly. The center of a concept can be defined to be the
normalized vector sum of all basis elements associated with themes
aggregated together to produce a synthetic concept.
Classification methods based on simple associative
neural networks are also possible. Once one or more KPU are created,
then a training set of documents can be used to encode a distributed
relationship between the class of natural kind and individual
documents. By altering the training presentation sequence and
rules, a single document can be associated with multiple concepts.
After training, new documents would be classified as concepts
within a specific view. Almost no computation, and almost no
computer memory, is required for classification using a trained
classifier engine, and thus the user, with proper software, could
quickly see the conceptual relationships that a document might
have in multiple views.
The derived formal model:
The procedure outlined above uses the power of the
Oracle ConText Option (OCO) to bypass the time intensive first
step in constructing a Pospelov type formal model. We defined
the formal model:
M1 = < T, P, A, R >
where T = a set of themes, P = { power set operator
P(.) on T}, A = {semantically correct elements of P(T)}, and R
= { compound semantic rule }.
We can now define the so called "derived model":
Md = < Td, Pd,
Ad, Rd >
This derived model can be developed by following
a procedure for deconstructing examples as outlined in Situational
Analysis.
By referring to Figure 5 the reader can following
the creation of the formal model M1 . J is
computed using ConText and a brief interaction with one or more
human experts. J is the base set of elements T for the
formal model M1 . Through validation procedures, a
class of natural kind N is identified by selecting from
the power set P(T). Initially this class is simply the axiom
set A.
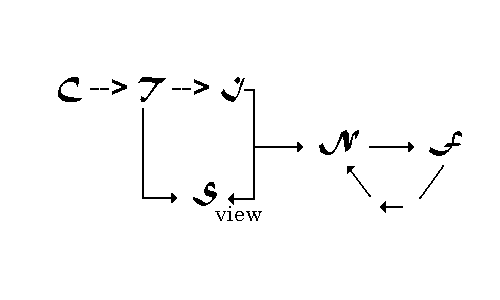
Figure 5: Knowledge
extraction and situational representation using a user defined
view.
The formal model M1 can be constructed
using existing software systems, Oracle's ConText plus some software
developed by Highland. However, more can be done once M1
exists. M1 contains a description, A, of meaningful
aggregations of subfeature representations of situations in the
world. Using this set of descriptions, it is possible to create
a theory of natural kind and a new set of subfeatures, Td
= F, where each of the elements of a natural class is modeled
as the emergent combination of subfeatures. The natural class
is initially modeled as being isomorphic to the set A.
The theory of natural kind is specified as a set,
Rd , of inference rules for determining the meaningfulness
of synthetic concepts, as well as the logico-transformation rules
governing how referential objects are formed in an external world.
A theory of natural kind is a deep result that can be appreciated
by examination of the work by M. Zabezhailo and V. Finn's work
on structural pharmacology. The logico-transformation rules is
a meta formalism that can be combined with the theory of plausible
reasoning as developed by logician Victor Finn.
Note that the logico-transformation rules are not
part of any formal model. Logico-transformation rules play an
important role in moving from a single formal model into a more
powerful semiotic model where transition between formal models
will be allowed. Logico-transformation rules are intended to
explain why a situation would arise as an example of a natural
kind.
The semantic rules, R, is a surface result that
provides a pragmatic way to delineate all, or most of, the natural
kind in a situation. Highland's strategic plan is to apply R
to build a classification engine for document management. This
will not require the development of a derived model where logico-transformation
rules are specified. The Knowledge Processing Project will, of
course, continue to be interested in the derived model, but this
system is simply more powerful than is required for vertical markets
needing advanced document management methods based on ontology.
Constructing N out of Rd and Td
may not be far away.
|