Predominant methodologies in doing science include the act of measuring (which involves an observable) and physically disassembling (or fractionating) a system. This section will show that if a system can be seen with multiple distinct observables, then it is not possible to physically separate (or fractionate) the system so that each fraction matches up exclusively with just one of the observables.

The central idea is that due to multiple observables, more can be seen in a system than can be physically fractionated out of the system. Consequently, if you only study the physical fractions, you will miss some of the behavior inducing semantics that was present in the intact system of interacting subsystems.

Index: [ Tutorial example #1 | Tutorial Example #2 | Subjective Illustration ]

-- Descriptions --

Tutorial example #1: the observables will match up with the fractions in a one-to-one way.
Tutorial example #2: the observables will not match up with the fractions in a one-to-one way.
Subjective Illustration: Illustration

Example #1: It is possible to cut (or fractionate) the picture to the left (of both women) in half creating two pictures (or physical fractions).

It is also possible to add or tape together each of the fractionated pieces (subsystems) to create the intact image (or system).

Next, consider looking at the intact combined picture so that your attention is focused only on the old woman. Call this the "old woman observable". Consider that any pattern that you don't recognize as an old woman, you see as just noise. An old man at his 60 year high school reunion looking for old female high school friends may employ such an observable. Consider that there is also a concurrent 10 year high-school reunion going on at the same facility so that there are also young people present. Consider that another person from the younger generation is trying to locate some of his female high school friends. He would utilize a "young woman observable". For his purposes, all patterns that he didn't recognize as a young woman would be essentially noise.

Glasses will symbolically be used to indicate an observable or "way of seeing" something.

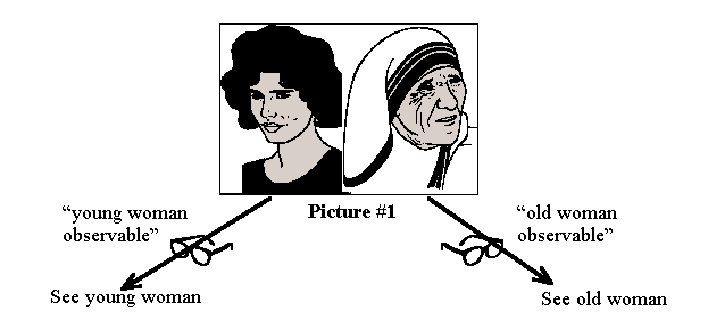
These observables have the effect of not seeing part of the whole picture. The old man ignores the young women. The young man ignores the old women. The consequences of these observables are the same as the fractionation process described earlier. These observables effectively separate the women into two distinct physical populations (young and old). This lead to the following observation.

With the above diagram (of both women), you can physically fractionate (or separate) the image of the young and old woman. You can also utilize the "young woman observable" to only see the young woman. Likewise, you can utilize the "old woman observable" to only see the old woman.

For this example, you can also take the analytical subsystems and add them together to create the original physical system. The analytic subsystems coincide with the physically fractionated subsystems. For this system the chosen observer-based analytic approach (as defined above) coincides with the physical fractionation approach described earlier. The converse, though, is not in general true. Although you can always separate analytically what you can separate physically, you can not always separate physically what you can separate analytically. Example #2 below will illustrate this.

Example #2. Consider looking at the following diagram, with the same observables (or glasses) as before.

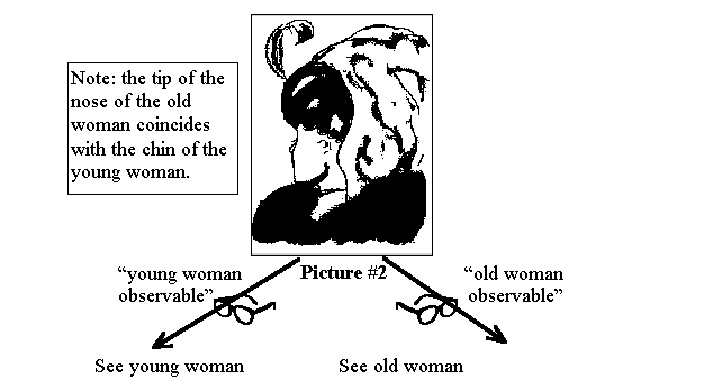
It is possible to analytically see two different observer-dependent recognizable patterns within the same physical image. Depending on how you look at the picture, you can either see a young woman or an old woman.

But note that it is not possible to physically fractionate out the image of the old woman from that of the young woman.

You cannot take a pair of scissors and cut the picture so that one part contains the old woman and the other part contains the young woman. You can not even partition the pixels (or minute points) of the picture so that one set of pixels contains only the image of the young woman and the other set contains only the image of the old woman. This means that there are pixels in the picture that have two different observer-based interpretations. In this case, what is ignored with each observable is another pattern in the same part of the physical image. Contrast this with the earlier example (picture #1) where what was ignored was a pattern in a different physical region of the image.

To illustrate these ideas further, consider fractionating further picture 1.

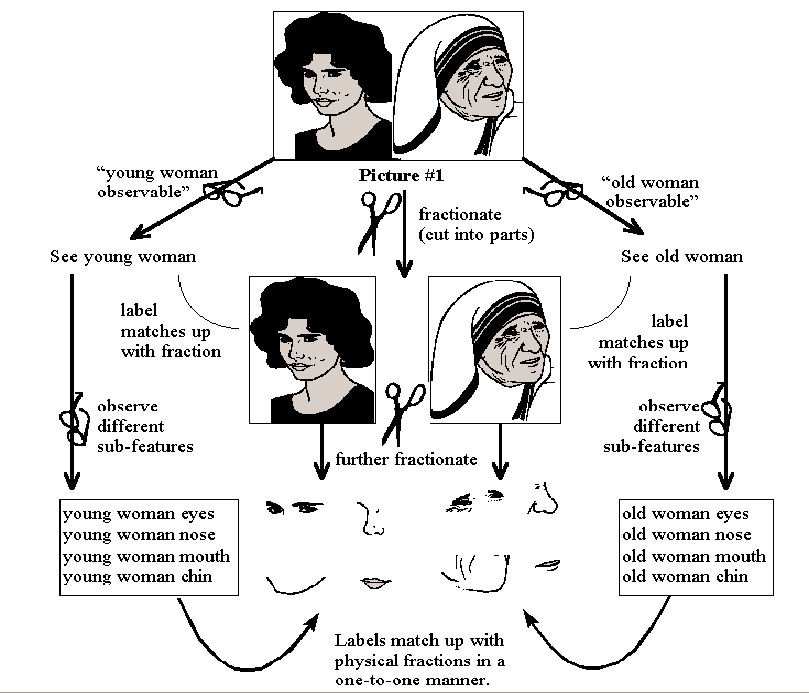
As noted before, this nice arrangement of analysis being identical with fractionation doesn't always hold.

One may now wonder if this isn't evidence for the subjective nature of observables. Well, observables are subjective (as related to the observer). The question is what happens in nature. If natural subsystems interact with other systems by the use of observables, then the use of subjective observables is essential to their understanding. A network of subsystems will be defined as complex, in line with Robert Rosens definition, if the observables used (by the subsystems) changes over time.

Mainstream reductionist science takes the position that all reference frames (or observables) are equivalent. Therefore, there should be no semantic information (or observer subjectivity) allowed. With this point of view it would be "bad science" to even identify a picture as an image of a young woman or an image of an old woman. All that is intrinsically present in the picture (according to the predominant scientific viewpoint) is lines and shading. Nothing else. All other semantic information is "observer added" and thus is not an intrinsic part of the picture. Contemporary science only deals with what is intrinsic to matter.

Since the 1950's starting with Rashevski, then later with Rosen, a complementary approach has been proposed called relational biology. The idea here is that what is of particular importance in biological systems is how subsystems interact (not what is intrinsic to an isolated part). Any time things interact, there is an observer and the observed (even in something as simple as a chemical reaction...one chemical observes another chemical in order to interact with it). Where there is an observer there is some observer added semantics. We identify fixed "laws of nature" or "equations of motion" whenever an observer is consistent in the way it observes something else. We tend to forget that observation is going on within the system. The point of relational biology is to provide a framework in which to study systems in which the internal observables are changing with time. We are hopeful that the integration of the Quasiaxiomatic-theory (QAT) of Victor Finn, the Applied Semiotics Systems of Demitry Pospelov and Robert Rosen's formalism will provide that framework.

-- End --